Creating ANTONBLAST's Layer Jump System
Crossposted from the ANTONBLAST kickstarter page
Heyo, it’s me, lovable lead programmer on ANTONBLAST Massimo Gauthier, here to talk about how I implemented the layer jumping mechanic! By following this simple guide, you too can become authentically inspired by 90s and 2000s era 2D platformers and their weird pseudo-3D gimmicks!
This system went through a few iterations throughout development (before I realized VB Wario Land was doing it better than me and just kinda copied how they did it). I'll just be focusing on how the final implementation works, so careful about making any inferences about how easy something like this is to build from scratch.
If you’re having trouble reading the code at any point, I’d recommend pasting into an empty script in Game Maker just to get the syntax highlighting. Substack seems to unfortunately not be great when it comes to code blocks.
Design Constraints
Starting out, here are the requirements and constraints for the layer system (laid out during the design stage or while experimenting with earlier iterations):
The game will only ever have 2 layers, a background and a foreground layer
A parallax effect is in place. We decided on a horizontal ratio of 0.5, meaning the camera will move about half as much on the background layer for any movement on the foreground layer. I'll expand a bit more on this later.
Anton can jump between layers by interacting with springs. Doing so will cause him to jump to a corresponding background/foreground position based on his position and the parallax adjustment.
Layer jumps always take the same amount of time.
Anton will virtually always land on the ground after layer jumping (there are a few acceptable exceptions, such as if no ground is available to land on).
The player has a small amount of horizontal control over a layer jump.
Anton will always appear to travel in a small vertical arc during a jump.
Parallax
Probably the most annoying thing to figure out and adjust for with layer jumping and basically everything else having to do with the layer system was the parallax. To summarize briefly, the true position (when it comes to collision and interaction) of things on the background layer does not correspond to their rendered position, as that has to be adjusted in order to create a parallax effect. Here's a Game Maker blog post explaining parallax in more detail. Normally this would not be such a big deal, but when you have stuff moving between layers that becomes an issue, as an object's true position according to the collision system can suddenly not correspond to where it's "supposed" to be according to what's actually being shown to the player. Usually this manifested as the object (Anton) snapping or warping around in strange ways after a layer jump.
To fix this, you have to take a position on one layer and convert it to a position on the other. Initially we were doing this in all sorts of places but I eventually consolidated things to a single function:
function parallax_adjust(_position, _backToForeground=false){
if(_backToForeground){
var _camPosAtPosition = (_position - VIEW_WIDTH/2)/PARALLAX_RATIO;
return round(_position + clamp(_camPosAtPosition, 0, room_width - VIEW_WIDTH)*PARALLAX_RATIO);
}
else{
return round(_position - clamp(_position - VIEW_WIDTH/2, 0, room_width - VIEW_WIDTH)*PARALLAX_RATIO);
}
}Let's break things down. This function takes an x position from one layer and converts to the equivalent x position on the other. You can specify with the second parameter whether you are converting from background to foreground or vice-versa. This might seem a little abstract, so I will now employ VISUAL LEARNING to help you conceptualize what is being done here. First, consider this example level layout (foreground elements are red and background elements are orange):
Here's what things look like for the player when Anton (technically, the camera following Anton) is fully on the left side of the stage:
No parallax is applied at this point, so the background's true and rendered positions are the same:
Now here’s what happens when Anton moves to the center of the stage. The background needs to move only half as slow as the camera. To achieve this effect, the background's rendered position (shown here in transparent grey) is set to be equal to its true position + the camera's current x position multiplied by the parallax ratio (0.5 in our case) (the camera's x position is the leftmost side of the black rectangle):
Here's what the player sees:
So, back to the conversion function. Basically what we're doing is running the rendering offset in reverse to get back the true position of whatever position we point at in the rendered background. Going step by step:
Foreground to background:
Take where the camera's position would be at the provided foreground position (
_position). This is just_positionminus half the camera's width (saved in the macroVIEW_WIDTH), with some clamping applied since the camera cannot move past the left or right edge of the room.Multiply this camera position by the
PARALLAX_RATIO(also a macro in this case). This gives you the background's rendering offset.Subtract this rendering offset from
_positionto get the true background position.
Background to foreground:
Pretty much the same steps as above, but a little more complicated since the camera's position here relative to
_positionis dependent on the parallax effect. To account for this, simply divide the camera position byPARALLAX_RATIObefore clamping it.You also need to add the rendering offset to
_positionhere instead of subtracting it to get the desired foreground position.
A Special Trick
Now that we've got a way of adjusting for parallax it's finally time to tackle the jump itself. Though you might be asking yourself at this point: "The parallax adjustment can only handle positions two layers! Isn't a jump supposed to smoothly move between them? How are you interpolating between the start and end positions?" This is in fact what I was trying to do at first. But then I discovered VB Wario Land's special trick. See if you can spot it in this gif where the player's collision mask is visible:
That's right, no physics interpolation is happening at all! As soon as the player initiates a jump, valid grounded position is identified and they are teleported there right away! The actual jumping Anton is just a rendered "ghost" that slowly approaches the true position. This has a number of useful advantages:
You can determine a valid grounded position before the jump even starts by doing the following:
Identify an initial target position using spring's center position adjusted using the parallax adjustment seen previously, as well as a y position slightly higher than the spring's (both of these "target" values can be overridden by the level designer if they want the spring to send you somewhere that isn't quite the exact position that corresponds to the spring's position).
If said target position would put the player inside terrain, move them up until they are just above it.
If said target position would put the player in midair, move them down until they are on top of terrain, with an exception if no terrain exists below.
Since you know the player will start in a valid position, you can give the player limited movement control using the existing speed and collision systems without worrying about them getting stuck in a wall or something. Because the ghost Anton is approaching the true position anyway, it takes minimal additional effort to allow this movement while still making it so both the ghost and true positions sync up at the end of a jump.
This allows you to know the relative heights of the player's initial and final position, which is invaluable for pre-calculating variables for a jump arc of fixed duration and height for the ghost Anton to follow.
The Jump Arc
The last big step before getting into the nitty gritty details is how to do the jump arc. As we all know, acceleration and deceleration can be modeled using the following kinematic equations:
d = distance
t = time
a = acceleration (or gravity)
f = final velocity
v = initial velocity
f = v + a*t
d = ((f + v)/2)*t
d = v*t + 0.5*a*t^2
f^2 = v^2 + 2*a*dEach half of the jump arc can be modeled by one of these equations. Here's what we know:
The final velocity of the first half and initial velocity of the second half, they're both 0 (i.e. the apex of the jump).
The highest point of the jump, which you can use to get the distance value for each half. You can determine the highest point by taking the higher of the starting or final y positions and subtracting a fixed offset (which can be adjusted by the designer). You then subtract the highest point from the starting and final y positions to get the distance values for each half of the jump.
The total time of the jump, which remains fixed by design.
Here's what we need to determine:
The time to the apex of the jump, which can then be used to get...
The gravity, which remains constant across both halves of the jump.
The initial velocity of the first half of the jump.
Since I wasn't able to figure out how to obtain those three variables mathematically, I wrote a bit of code to brute force the problem. This doesn't really affect much performance-wise but if anyone knows how to solve this properly do let me know. Here is the code in question (the y variable here refers to the target y position, which was determined earlier):
var _layerJumpHighPoint = min(_startY, y) - layerJumpHeight;
var _fallDistance = y - _layerJumpHighPoint;
var _jumpDistance = _startY - _layerJumpHighPoint;
layerJumpGrav = 0;
var _currentJumpTime = 999;
while(_currentJumpTime > layerJumpTime){
layerJumpGrav += 0.01;
var _timeToApex = sqrt(2*_jumpDistance/layerJumpGrav);
layerJumpVerticalSpeed = -layerJumpGrav*_timeToApex;
_currentJumpTime = _timeToApex + sqrt(2*_fallDistance/layerJumpGrav);
}The Details
Now that all the big conceptual stuff is out of the way, all that's left to go over is the specific implementation details. Please note that some edits have been made to code snippets keep things focused on the essential functionality, you guys don't need to know the filename for every sound Anton is making while jumping. Also to note, the player object uses a finite state machine, I won't go in-depth on that pattern so here's a good explanation of how it works for those unfamiliar.
Let's start with the variables used on the player object:
layerJumpHeight = 25;
layerJumpX = -1;
layerJumpY = -1;
layerJumpVerticalSpeed = 0;
layerJumpGrav = 0;
layerJumpTime = 50;
layerJumpTimer = -1;
layerJumpMaxHorizontalSpeed = 1;"Height" is the offset used to determine the peak of the jump during the arc calculation. We measure units of distance in pixels, native screen size is 384x216.
"X" and "Y" here are used to keep track of the Anton "ghost"'s render position during the jump.
As we saw earlier, "Grav" and "VerticalSpeed" are determined during the jump arc calculation and affect the shape of the jump arc.
"Time" determines how long a jump takes in frames (at 60 FPS the value given above would be about 0.83 seconds)
"Timer" keeps track of how long the player has been in a layer jump. While the end of the jump is not triggered by the timer, it is still useful for other things we'll see later.
"MaxHorizontalSpeed" determines how fast the player can move from side to side during a layer jump.
The player triggers a layer jump by standing on a spring in the normal state and jumping (we also check that they aren't holding left or right):
if (jump){
var _spring = instance_place(x, y+1, mySpring);
if(!moveLeft && !moveRight && _spring != noone){
layerJump(_spring.targetX, _spring.targetY);
}
}layerJump = function(_targetX, _targetY){
myLayer = (myLayer == 0) ? 1 : 0;
currentState = playerStates.playerLayerJump;
horizontalSpeed = 0;
verticalSpeed = 0;
if(myLayer == 0) layerJumpX = round(x + camera_get_view_x(PLAYERVIEW)*PARALLAX_RATIO);
else layerJumpX = round(x - camera_get_view_x(PLAYERVIEW)*PARALLAX_RATIO);
var _startY = y;
x = _targetX;
while(
place_meeting(x, _targetY, myBlock) ||
place_meeting(x, _targetY, myPassthrough)
){
_targetY -= 1;
if(_targetY < 0){
_targetY = y;
break;
}
}
y = _targetY;
while(
!(check_below(_targetY) ||
check_below_passthrough(_targetY))
){
_targetY += 1;
if(_targetY > room_height){
_targetY = y;
break;
}
}
y = _targetY;
var _layerJumpHighPoint = min(_startY, y) - layerJumpHeight;
var _fallDistance = y - _layerJumpHighPoint;
var _jumpDistance = _startY - _layerJumpHighPoint;
layerJumpGrav = 0;
var _currentJumpTime = 999;
while(_currentJumpTime > layerJumpTime){
layerJumpGrav += 0.01;
var _timeToApex = sqrt(2*_jumpDistance/layerJumpGrav);
layerJumpVerticalSpeed = -layerJumpGrav*_timeToApex;
_currentJumpTime = _timeToApex + sqrt(2*_fallDistance/layerJumpGrav);
}
layerJumpY = _startY;
layerJumpTimer = 0;
}The layer jump function does a bunch of setup:
Changes the player's layer
Puts the player in the layer jump state
Zeroes out the player's speed
Sets the Anton ghost's initial render position based on the player's current pre-jump position
Determines a valid position based on the desired target coordinates and teleports the player there
Resets the jump timer
Calculates the jump arc, as seen earlier
Once the player object is in the layer jump state, it'll start running this code in its step event:
layerJumpX = approach(layerJumpX, x, 0.4);
layerJumpX += horizontalSpeed;
var _moveDir = moveRight - moveLeft;
horizontalSpeed = layerJumpMaxHorizontalSpeed*_moveDir;
verticalSpeed = 0;
layerJumpVerticalSpeed += layerJumpGrav;
if(layerJumpVerticalSpeed < 0) layerJumpY += layerJumpVerticalSpeed;
else{
layerJumpY = approach(layerJumpY, y, layerJumpVerticalSpeed);
if(layerJumpY == y){
if(!onGround) verticalSpeed = layerJumpVerticalSpeed;
currentState = playerStates.playerNormal;
}
}
layerJumpTimer++;
Said code does the following:
Approach the render position to the player's true position, such that they're guaranteed to sync up before the jump ends.
Move the render position based on the player's movement speed.
Lets the player move left and right based on the layer jump horizontal speed. This should be done after the previous step to allow collision, which would usually run after this, to properly affect the speed being applied to the render position.
Keeps vertical speed at 0, eliminating the normal physics' gravity. Leaving gravity on would cause various issues given this implementation, and it coming into play at all is enough of an edge case that I decided it would be easiest to just disable it.
Does the usual physics stuff with gravity and vertical speed to the ghost.
Once the ghost is on its way down, checks whether it's reached the target y position. Once it has it transitions the player back to their normal state.
Last but not least, let's take a look at the code that's rendering all this:
if(currentState == playerStates.playerLayerJump){
var _scale = map(layerJumpTimer, 0, layerJumpTime, (myLayer == 1) ? 0.5 : 1, spriteScale);
_drawX = round(layerJumpX + ((myLayer == 0) ? 0 : (camera_get_view_x(PLAYERVIEW)*PARALLAX_RATIO)));
var _palette = map(_scale,0.5,1,2,1);
pal_swap_set(playerPalette,_palette,false);
draw_sprite_ext(
sprite_index, image_index,
_drawX, round(layerJumpY),
_scale, _scale, image_angle, image_blend, image_alpha
);
}
Going line-by-line:
The player's scale is smoothly adjusted using the layer jump timer as they transition to or from the background.
The draw position is determined by taking the render position and adjusting for parallax based on whether the player is in the background or not (remember, the new layer value is set as soon as a jump is initiated).
The player's palette is also subtly adjusted (based on their scale) as they change layers to create an atmospheric scattering lighting effect.
The player's sprite is then drawn using the values we have painstakingly calculated.
Extra Tidbits on Keeping the Player in the Background
To avoid this post getting too long, I'll be brief with this stuff, especially since it shouldn't be too hard for others to figure out the details. For the most part the player works the same while they're in the background, with a few notable exceptions:
Like other objects that appear both in the foreground and background, Anton is rendered at half size while in the background, and his collision mask is also adjusted to match.
The player object's physics variables are halved to keep the movement correct despite the player's small size
The player object can only collide with things on the same layer as it. Our current implementation of this is pending a complete rewrite. My intent is to replace the collision functions with ones that have the layer check built-in, perhaps using collision matrices similar to unity.
Conclusion
Well there you have it, all the information you need to totally rip us off as badly as we ripped off, uh, a bunch of stuff actually. There's a surprising amount of platformers that have a gimmick like this. Guess that speaks to its strength as a level design tool! If you have any questions feel free to leave a comment or join our discord and ask in the #your-computer channel, which I hang around in regularly. Thanks for reading, see you next devlog! Oh, and be sure to check out the kickstarter page!


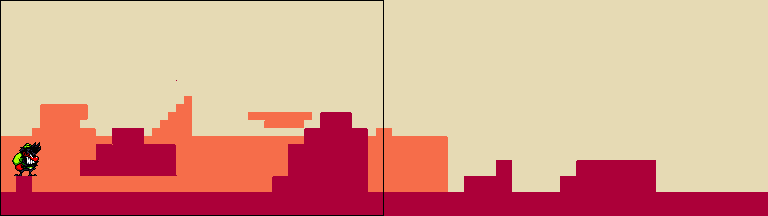



I really enjoyed this post! I think I have a direct solution to solve for gravity. Sorry, I didn't bother to make it pretty.
So basically, we have this, which was obtained by plugging in the expression for _timeToApex into the expression for _currentJumpTime:
_currentJumpTime = sqrt(2*_jumpDistance/layerJumpGrav) + sqrt(2*_fallDistance/layerJumpGrav);
In the loop, we want to get _currentJumpTime to equal layerJumpTime (which is known), so replace _currentJumpTime with layerJumpTime, noting that _jumpDistance and _fallDistance are already known:
layerJumpTime = sqrt(2*_jumpDistance/layerJumpGrav) + sqrt(2*_fallDistance/layerJumpGrav);
Factor out sqrt(1/layerJumpGrav):
layerJumpTime = sqrt(1/layerJumpGrav)*(sqrt(2*_jumpDistance) + sqrt(2*_fallDistance));
Muliply both sides by sqrt(layerJumpGrav):
layerJumpTime*sqrt(layerJumpGrav) = sqrt(2*_jumpDistance) + sqrt(2*_fallDistance);
Divide both sides by layerJumpTime:
sqrt(layerJumpGrav) = (sqrt(2*_jumpDistance) + sqrt(2*_fallDistance))/layerJumpTime;
square both sides:
layerJumpGrav = ((sqrt(2*_jumpDistance) + sqrt(2*_fallDistance))/layerJumpTime)^2;
Now, once you have layerJumpGrav, you can find layerJumpVerticalSpeed and _timeToApex